旋转矩阵与李群李代数
旋转矩阵
旋转矩阵是3D空间中任意旋转的表示,一般来说旋转矩阵R的维度为3x3,可以表示一个笛卡尔坐标轴相对于另一个笛卡尔坐标轴的任意旋转,在一般的机器人学中,用于表示关节之间的旋转关系
最经典的旋转矩阵为
1 | R = \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} |
代表一个绕$Z$轴旋转的任意角度为$\theta$的旋转矩阵
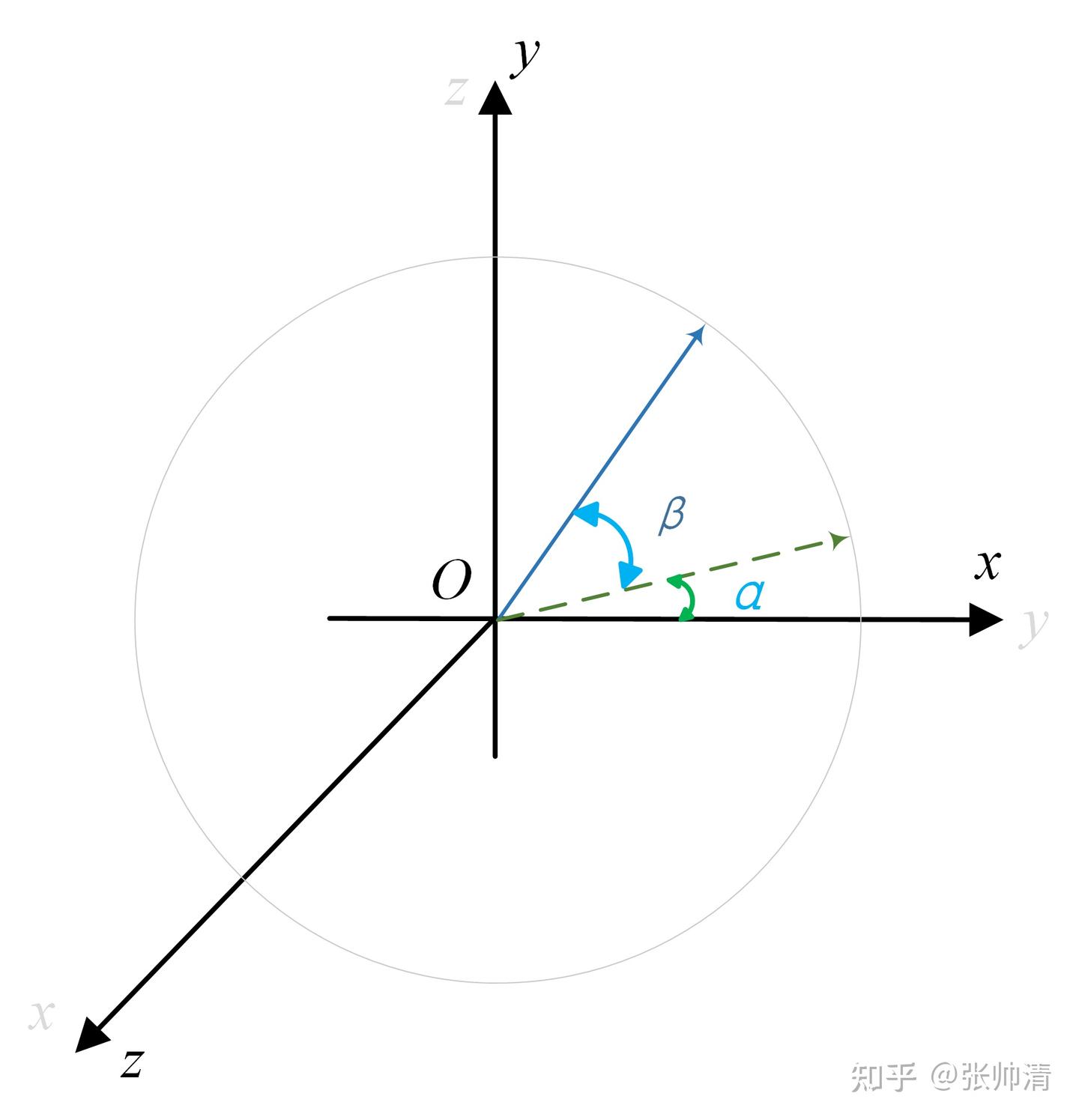
具体在$R$中每个位置旋转的意义可以参考我手写的笔记
同时考虑在实际情况中将旋转和移动Mapping到3D空间中,那么这个表示变换维度变为4x4,那么齐次变换矩阵的表示为
1 | T = \begin{bmatrix} R & P \\ 0 & 1 \end{bmatrix} |
其中$R$为旋转矩阵,$P$为平移向量,对于某个点$P_A$,通过齐次变换为$P_B$,平移向量为$P_A^B$,有
1 | \begin{bmatrix}P_B \\ 1 \end{bmatrix} = \begin{bmatrix} R_A^B & P_A^B \\ 0 & 1 \end{bmatrix} \begin{bmatrix}P_A \\ 1 \end{bmatrix} |
通过建立关节(joint)之间的旋转和平移关系,我们可以后续建立对应的正向运动学(通过各关节物理量求出末端位置)和逆向运动学(通过末端位置结算出求出满足的各关节物理量)
李群与李代数
李群跟李代数在计算机图形学,机器人学中的使用非常广泛,其中李群主要定义了满足某一集合代数操作的集合,而李代数则定义了该集合的代数操作,比如李群中定义的旋转矩阵,而李代数中定义了对应李群的代数操作,比如微分,求导等
关于李群和李代数的定义,可以参考
写给计算机系同学的李群与李代数(一):从旋转矩阵到抽象群
简单的说我们在前面定义的旋转矩阵,无论是二维还是三维,都满足了李群的定义,也就是对应一个三维旋转矩阵,定义了在空间中任意旋转变换的集合,所以对一个基座矩阵,将所以旋转矩阵再作用一个单位向量,得到的是一个在空间中的单位圆。
而李代数可以将旋转的角度求导得到旋转速度,也就是“无穷小变化”